개념
1. 스택 (Stack)
입력과 출력을 한방향에서 제한한 자료 구조이다. LIFO(Last in First Out)으로 가장 나중에 들어온 데이터가 먼저 빠져 나가는 구조이다. 파이썬에서는 리스트를 사용해 스택을 구현할 수 있습니다.
stack = []
stack.append(1) #삽입
stack.append(2)
stack.pop() #삭제 => 2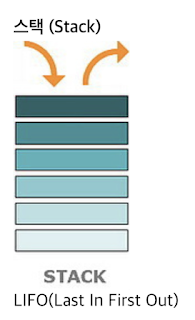
2. 큐 (Queue)
한쪽 끝에서만 자료를 넣고 뺄 수 있는 자료구조이다. FIFO(First in First Out)구조로 처음으로 저장된 데이터를 처음 사용하는 방식이다.
(스택과 달리 큐를 list로 사용하지 않는 이유는 pop()의 시간복잡도 O(1) < pop(0)의 시간 복잡도는 O(N)이기 때문입니다.)
import queue
q = queue.Queue()
q.put(1) #삽입
q.put(2)
q.get() # 삭제 => 1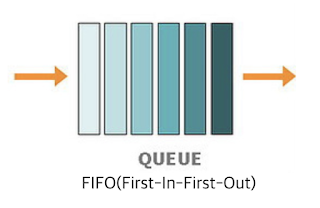
3. 덱 (deque)
양쪽 끝에서 자료를 넣고 뺄 수 있는 자료구조이다. 덱을 이용하면 스택과 큐를 구현 할 수 있습니다.
from collections import deque
q = deque()
q.append(1) # 오른쪽 끝에 삽입
q.append(2)
q.popleft() # 왼쪽 끝 값 가져오는 동시에 삭제 => 1
q.pop() # 오른쪽 끝 값 가져오는 동시에 삭제 => 2
q.appendleft(0) # 왼쪽 끝에 삽입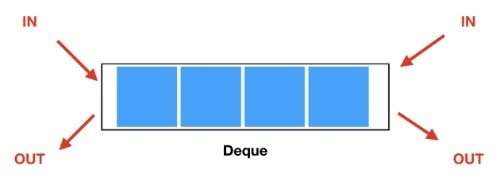
문제 설명
프로그래머스 팀에서는 기능 개선 작업을 수행 중입니다. 각 기능은 진도가 100% 일 때 서비스에 반영할 수 있습니다.
또, 각 기능의 개발속도는 모두 다르기 때문에 뒤에 있는 기능이 앞에 있는 기능보다 먼저 개발될 수 있고, 이때 뒤에 있는 기능은 앞에 있는 기능이 배포될 때 함께 배포됩니다.
먼저 배포되어야 하는 순서대로 작업의 진도가 적힌 정수 배열 progresses와 각 작업의 개발 속도가 적힌 정수 배열 speeds가 주어질 때 각 배포마다 몇 개의 기능이 배포되는지를 return 하도록 solution 함수를 완성하세요.
제한 사항
- 작업의 개수(progresses, speeds배열의 길이)는 100개 이하입니다.
- 작업 진도는 100 미만의 자연수입니다.
- 작업 속도는 100 이하의 자연수입니다.
- 배포는 하루에 한 번만 할 수 있으며, 하루의 끝에 이루어진다고 가정합니다. 예를 들어 진도율이 95%인 작업의 개발 속도가 하루에 4%라면 배포 는 2일 뒤에 이루어집니다.
입출력 예
| progresses | speeds | return |
| [93,30,55] | [1,30,5] | [2,1] |
입출력 예 설명
첫 번째 기능은 93% 완료되어 있고 하루에 1%씩 작업이 가능하므로 7일간 작업 후 배포가 가능합니다.
두 번째 기능은 30%가 완료되어 있고 하루에 30%씩 작업이 가능하므로 3일간 작업 후 배포가 가능합니다. 하지만 이전 첫 번째 기능이 아직 완성된 상태가 아니기 때문에 첫 번째 기능이 배포되는 7일째 배포됩니다.
세 번째 기능은 55%가 완료되어 있고 하루에 5%씩 작업이 가능하므로 9일간 작업 후 배포가 가능합니다.
따라서 7일째에 2개의 기능, 9일째에 1개의 기능이 배포됩니다.
나의 풀이
deque FIFO을 활용한 풀이 (통과)
import math
from collections import deque
def solution(progresses, speeds):
result = deque()
for i in range(len(progresses)):
result.append(math.ceil((100-progresses[i])/speeds[i]))
cnt = 1
answer = []
max = result.popleft()
while len(result) != 0:
if max < result[0]:
answer.append(cnt)
cnt = 1
max = result.popleft()
else:
cnt+=1
result.popleft()
answer.append(cnt)
return answer
- 작업마다 걸리는 일수를 result 덱으로 정의 (덱을 선택한 이유는 앞에 있는 기능이 먼저 순차적으로 배포되어서 꺼내지기 때문에 FIFO)
- 작업의 진도 만큼 for 문을 돌려 100(전체 진도)에서 진도율을 빼면 남은 일의 양이 나옵니다. 앞에서 구한 값을 개발 속도로 나누면 걸리는 일수가 나옵니다. 또한 만약에 7.3일이 나오면 8일이 걸리기 때문에 올림을 해줍니다. ( 일수 = 작업량 / 시간당 작업량) 이를 앞에서 정의한 result에 넣어 줍니다.
- answer에 며칠째에 몇 개의 기능이 배포되는지를 저장하기 위해 리스트 변수로 선언하였습니다. cnt는 하루에 같이 배포는 기능을 누적시키기 위한 변수입니다. 또한 cnt는 하루에 적어도 1개는 배포되기 때문에 1로 초기화 하였습니다. max는 작업마다 걸리는 일수 중 선행 되어야 하는 값에서 최댓값이라는 의미로 max로 선언을 하였습니다.
- if 문에서
4-1. max보다 뒤의 값이 더 크면 같이 하루에 배포될 수 없기 때문에 answer에 cnt를 넣어줍니다. cnt는 1로 다시 초기화시킵니다. 앞의 기능이 배포가 먼저 되었기 때문에 그다음 기능을 뒤의 기능과 비교하기 위해 popleft()를 통해서 꺼내서 max에 대입합니다.
4-2. max보다 작거나 같으면 같이 하루에 같이 배포될 수 있기 때문에 cnt의 값을 증가시킵니다. 그다음 값을 비교하기 위해 popleft()를 통해서 값을 지웁니다. - 마지막으로 넣어야 하는 cnt값은 계산만 하고 안 넣기 때문에 while 문을 탈출한 후 값을 answer에 넣습니다.
